- Index
- index
- README
- Sommaire Informatique
- Sommaire Maths
- Sommaire Chimie
- Sommaire Physiques
- Régime transitoire
- Nombres complexes
- Formules de Taylor
- Espace vectoriel
- Séries numériques
- Loi de composition
- variables et opérations
- Régime pseudo-périodique
- Bases locales
- Matrices
- Probabilités
- Suites numériques
- Comparaisons locale de fonctions
- Relation binaire
- Intégration
- Continuité
- Sommes et produits
- Nombres quantiques
- Ensembles
- Théorème des gendarmes
- Ondes acoustiques
- Champs de vecteurs
- Ecriture complexe et Impédances
- Intégration discrète
- Valeur propre
- Lambda-Calcul
- Fonctions hyperboliques
- Pivot de Gauss
- Dérivée
- Calcul Polynomial
- Binôme de newton
- Configuration Atomique
- Logique
- Nabla
- Fonctions de la variable réelle
- Déterminants
- Laplacien
- lancer un programme
- Série de Reimann
- Ondes mécaniques
- Schéma de Thévenin-Norton
- Divergence
- Fonctions trigonométriques
- Gradient
- Développements généralisés
- Développements limités
- Systèmes de coordonnées
- Reduction d'endomorphisme
- Méthode Acide-Bases
- Nomenclature
- Raisonnements logiques
- Structure de groupes
- Intervalle et voisinage
- Théorème des accroissements finis
- Applications linéaires
- Régime apériodique
- Energie d'ionisation
- Analyse Vectorielle
- Constante d'équilibre
- Equations différentielles linéaires
- Systèmes linéaires
- Fractions rationnelles
- Décomposition en éléments simples
- Puissance Electrique
- Oscillateur Harmonique
- Polynomes
- Preuve GL est un groupe
Oscillateur Harmonique
Définition
Un oscillateur harmonique est un model idéal d'oscillateur dont l'évolution est défini par une fonction sinusoïdale pouvant être définit uniquement par les conditions initiales.Les oscillateurs sont en réalité des cas particuliers des équations différentielles du second ordre.
OH simple
Que l'on considère un circuit électrique ou un système mécanique, si on étudie une oscillation parfaite et sans amortissement, on cherche une équation différentielle de la forme :\[ \ddot x + \omega_0^2x = \lambda \]
Avec \(\omega, \lambda\) des constantes réelles.
On appel alors \(\omega_0\) la pulsation propre. C'est la `fréquence` de l'oscillation, a une multiplication par \(\pi\) près.
La résolution simple donne :
\[ \begin{align} x(t) &= Acos(\omega_0t + \phi) + \Delta_0 \\ \Delta_0 &= {\lambda \over \omega^2} \end{align} \]
On auras donc un graph de la forme :
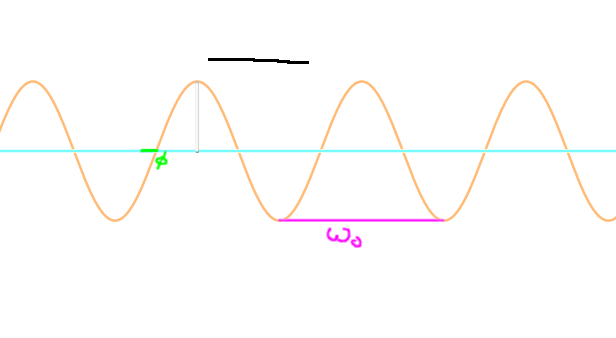
Voici un exemple de résolution avec un système masse ressort
Pour se ramener a une équation nulle, il peut être utile de considérer l'élongation \(u = x - x_0\). Ainsi, on obtient :
\[ \begin{align} \ddot u + w^2u &= 0 \\ u(t) &= Acos(w_0t + \phi) \end{align} \]
OH amortie
Dans le monde réel, un oscillateur harmonique perd de l'énergie a chaque oscillation. On appel cela, l'amortissement.
Celui ci est proportionnel a la `vitesse`, c'est a dire a la dérivé de la quantité étudiée. On pose alors une seconde force, \(F\), dans le sens contraire de la vitesse.
\[ F = -\mu \dot x \]
On a alors deux forces qui s'appliques sur notre système. La force de l'oscillation (le ressort ou la bobine/condensateur) ainsi que la force
d'amortissement (la friction ou la résistance).
On considère ici l'[analogie électro mécanique](https://fr.wikipedia.org/wiki/Analogie_%C3%A9lectro-m%C3%A9canique)
Ainsi, dans la suite, on décrira la masse pour parler a la fois de masse et d'inductance, ainsi que la friction pour parler de la friction mécanique ou de la résistance électrique.
On a alors une équation différentielle de la forme :
\[ \ddot x + {\omega_0 \over Q} \dot x + \omega_0^2 x = 0 \]
Où \(Q\) est tel que:
\[ {\omega_0 \over Q} = {\mu \over m} \Rightarrow Q = {m \omega_0 \over \lambda} \]
On rappel que \(m \sim L\); \(\mu \sim R\)
Résolution
On a alors une équation différentielle du second ordre de la forme :\[ a\ddot y + b\dot y + cy = 0 \]
On suit donc la méthode classique.
L'équation caractéristique donne :
\[ ar^2 + br + c = 0 \]
donc
\[ \Delta = b^2 - 4 a c \]
On remarque par ailleurs[^1], que le signe de \(\Delta\) est dirigé par la valeur de \(Q\) par rapport a \(1 \over 2\). On distingue donc trois cas :
1. Régime pseudo-périodique (\(\Delta < 0 \Leftrightarrow Q > {1 \over 2}\))
2. Régime apériodique (\(\Delta > 0 \Leftrightarrow Q < {1 \over 2}\))
3. Régime critique (\(\Delta = 0 \Leftrightarrow Q = {1 \over 2}\))
[^1]: cours en ligne tres util