- Index
- index
- README
- Sommaire Informatique
- Sommaire Maths
- Sommaire Chimie
- Sommaire Physiques
- Régime transitoire
- Nombres complexes
- Formules de Taylor
- Espace vectoriel
- Séries numériques
- Loi de composition
- variables et opérations
- Régime pseudo-périodique
- Bases locales
- Matrices
- Probabilités
- Suites numériques
- Comparaisons locale de fonctions
- Relation binaire
- Intégration
- Continuité
- Sommes et produits
- Nombres quantiques
- Ensembles
- Théorème des gendarmes
- Ondes acoustiques
- Champs de vecteurs
- Ecriture complexe et Impédances
- Intégration discrète
- Valeur propre
- Lambda-Calcul
- Fonctions hyperboliques
- Pivot de Gauss
- Dérivée
- Calcul Polynomial
- Binôme de newton
- Configuration Atomique
- Logique
- Nabla
- Fonctions de la variable réelle
- Déterminants
- Laplacien
- lancer un programme
- Série de Reimann
- Ondes mécaniques
- Schéma de Thévenin-Norton
- Divergence
- Fonctions trigonométriques
- Gradient
- Développements généralisés
- Développements limités
- Systèmes de coordonnées
- Reduction d'endomorphisme
- Méthode Acide-Bases
- Nomenclature
- Raisonnements logiques
- Structure de groupes
- Intervalle et voisinage
- Théorème des accroissements finis
- Applications linéaires
- Régime apériodique
- Energie d'ionisation
- Analyse Vectorielle
- Constante d'équilibre
- Equations différentielles linéaires
- Systèmes linéaires
- Fractions rationnelles
- Décomposition en éléments simples
- Puissance Electrique
- Oscillateur Harmonique
- Polynomes
- Preuve GL est un groupe
Continuité
calculus
Définition
Soit une fonction \(f\) définie sur \(D\) un intervalle de \(\mathbb{R}\), on dit que celle-ci est continue en \(x_0\) si :- elle admet une limite a droite en \(x_0\)
- elle admet une limite a gauche en \(x_0\)
- \(\lim_{x\to x_0^-} f(x) = \lim_{x \to x_0^+} f(x)\)
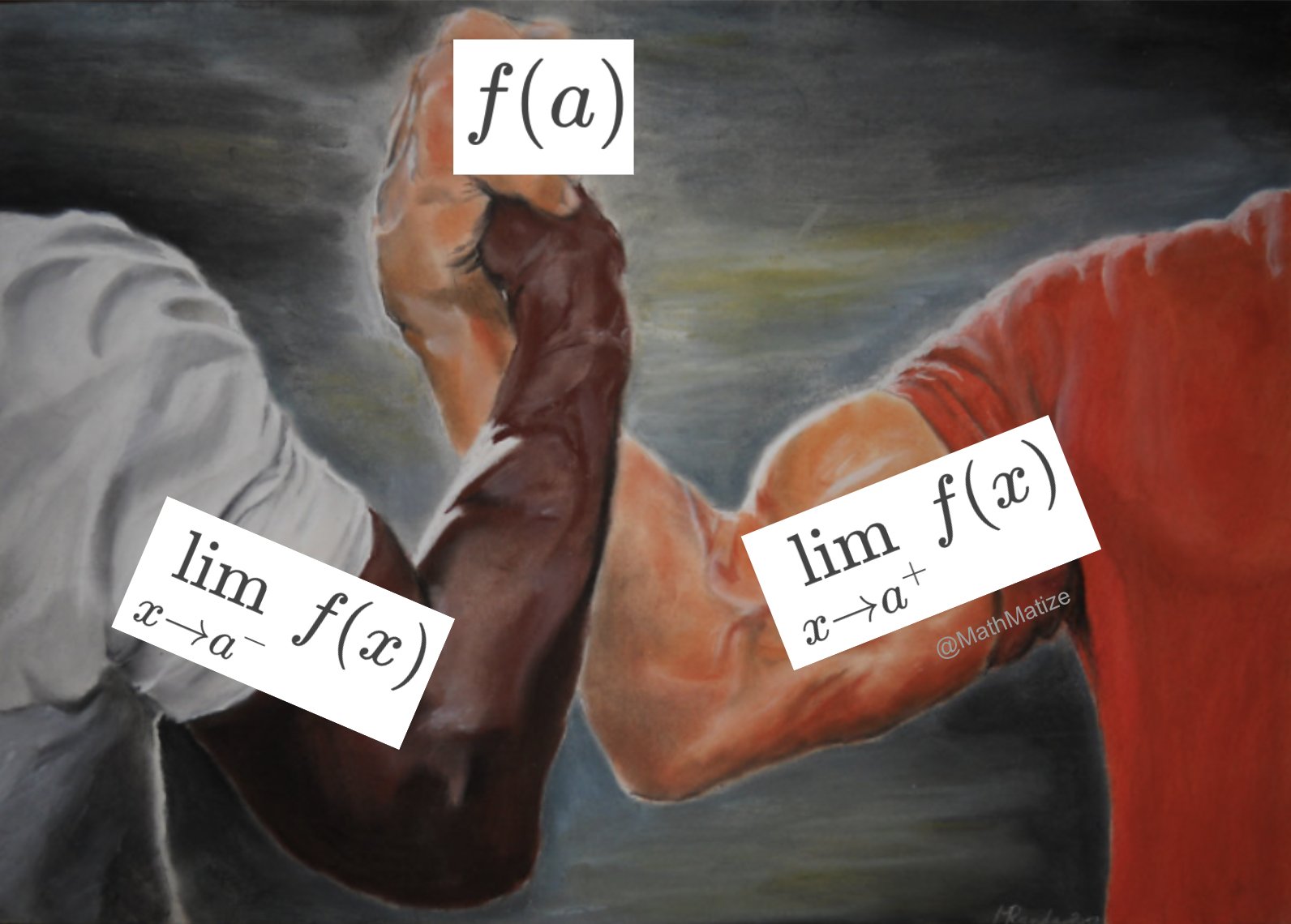
Si une fonction n'est pas continue, on dit qu'elle est discontinue.
Il existes différentes Espèces de discontinuités.
Définition des limites finies
Soit la fonction \(f\) définie sur \(D\), on dit que \(f\) admet une limite en \(x_0\) si\[ \forall \epsilon > 0, \exists \mu > 0, \forall x \in D, |x - x_0| < \mu \Rightarrow |f(x)-f(x_0)| < \epsilon \]
En des termes plus compréhensibles,
Pour toute précision \(\epsilon\), il doit exister une précision \(\mu\) sur les antécédent tel que les images des antécédents autour de \(x_0\) a \(\mu\) près, sont toutes a \(\epsilon\) près de \(f(x_0)\)
Ainsi, si \(f\) admet une limite en \(x_0\), celle ci vaux \(f(x_0)\)
Prolongement par continuité
On considère \(f\) discontinue d'ordre 1, cet a dire que ses limites a gauche et a droite de \(x_0\) sur \(D \backslash \{x_0\}\) sont finis. Si ses limites a gauche et a droite de \(x_0\) sont égales, on dit que \(f\) est prolongeable par continuité.Cet a dire qu'on peut poser une fonction \(\tilde f\) défini par :
\[ \tilde f(x)= \begin{cases} f(x),& x \ne x_0 \\ \lim_{x \to x_0} f(x), & \text{otherwise} \end{cases} \]
Un exemple utile en physique est la fonction sinus cardinal
\[ S(x) = {sin(x)\over x} \]
\(S\) n'est pas défini en 0, mais on la prolonge par continuité tel que :
\[ \tilde S(x)= \begin{cases} {sin(x)\over x},& x \ne 0 \\ 1, & x = 0 \end{cases} \]
Caractérisation séquentielle
Parfois, pour étudier la limite d'une fonction en un point \(x_0\), il est plus facile de le faire via une suite qui tend vers \(x_0\). Ce procédé s'appelle la caractérisation séquentielle. Le théorème s'écrit ainsi :\[ f \text{ admet une limite } l \text{ en } x_0 \Leftrightarrow \{ \forall(u_n)_{n\in \mathbb{N}}, \lim u_n = x_0 \Rightarrow \lim f(u_n) = l \} \]
Dans la pratique, cela sert surtout a prouver qu'une fonction est discontinue en un point, en utilisant les suites extraites.